Relative Velocity
-
Continued from the previous thread...
An aircraft flies due east from A to B where AB = 200km. The wind is blowing from the direction 030° at 60km/h. The speed of the aircraft in still air is 300km/h and the pilot sets the course on the bearing X°. Find
a) the value of X.
b) the time taken, in minutes for the journey from A to B. -
Given:Originally posted by Y_Shun:Continued from the previous thread...
An aircraft flies due east from A to B where AB = 200km. The wind is blowing from the direction 030° at 60km/h. The speed of the aircraft in still air is 300km/h and the pilot sets the course on the bearing X°. Find
a) the value of X.
b) the time taken, in minutes for the journey from A to B.
Due east is 090°, which is the actual route the aircraft supposed to take (I assume that from the not-so-good english of the question)
Wind is blowing at 030° at 60km/h
U can draw as shown:
Draw the black first... 2 arrow heads mean resultant that we want
Then draw green colour. Notice that they have the same starting point, and both arrows go away
Then red colour is the one that the plane should fly towards the destination.
From there, you should be able to find x using angles and triangles. Then you can find the speed of black colour vector by cosine rule.
*****************************************************
However if you want a lazy method, you can do this.
Resolve green one into vertical and horizontal:
vert: 60 cos 30°
hort: 60 sin 30°
Resolve red one into vertical and horizontal:
vert: 300 cos y°
hort: 300 sin y°
where y = 180 - x
U will realise that the horizontal direction of both vectors is in the direction where we want them. Also, the vertical motion of the final vector is zero. Which means
60 cos 30° = 300 cos y°
cos y° = sqr(3) / 10
y° =80°
which gives you x° = 100°
From here, you can find the speed = 60sin 30° + 300 sin y° = 325km/h
Unclebutcher pls check for me... Today my turn to have studied overnight without sleeping yet... May hv lots of careless mistakes...
Ok time to continue chionging my optoelectronics... -
ty for ur help anyway...but ans wrong...
X = 80
Time taken = 45min... -
sry I read wrongly...Originally posted by Y_Shun:ty for ur help anyway...but ans wrong...
X = 80
Time taken = 45min...
The wind is blowing from... not towards...
Do the same thing, change the direction of the green arrow... And try again
then tell me if it's correct... -
but your X is still labled wrongly riht?
if its 80, your angle there is defintely more than 90... -
my diagram is already wrong... The general idea is there...Originally posted by Y_Shun:but your X is still labled wrongly riht?
if its 80, your angle there is defintely more than 90...
Try to understand and redraw a diagram of your own... Or do u need help to draw again? -
just for you to check...

-
Resolve green one into vertical and horizontal:
vert: 60 cos 30°
hort: 60 sin 30°
Resolve red one into vertical and horizontal:
vert: 300 cos x°
hort: 300 sin x°
a)
vertical component = 0
60 cos 30° = 300 cos x°
cos x° = 0.2 cos 30°
x° = 80°
b)
horizontal speed = 300 sin x° - 60 sin 30° = 265.4 km/h
time taken = 200/265.4 = 0.75 hrs -
Resolve green one into vertical and horizontal:
I dun understand this part leh...
vert: 60 cos 30°
hort: 60 sin 30°
Resolve red one into vertical and horizontal:
vert: 300 cos x°
hort: 300 sin x° -
we are talking about vectors...Originally posted by Y_Shun:I dun understand this part leh...
In vectors, we can resolve everything into 2 other vectors (due to triangular sum of vectors)
The easiest way is to resolve everything into vertical and horizontal.
Notice that the final velocity is horizontal... This tells us that the vertical component is zero. Bear in mind that black arrow tells us the resultant of the green and red. Hence, the vector sum of the green vertical component and the red vertical component should be zero. The trick here is not really to bother about positive or negative signs in the equations, as what you should do in physics, but to use the magnitudes, and then determine the directions yourself using the arrows. It is easier on the calculations and mental thinking this way. -
ok neh minds, i ask another qtn
An aircraft is flying due south at 350km/h.
is this VA or is this VA/W? -
What do mean by VA or is this VA/W?Originally posted by Y_Shun:ok neh minds, i ask another qtn
An aircraft is flying due south at 350km/h.
is this VA or is this VA/W?
And is this question related to the above question? Pls do not give part of a question; it misleads pple
The most important thing in relative velocity is to understand the concept of vectors... It's rather hard to explain through a forum... You need someone experienced to guide you through at least a few tys questions before catching it (fast way). -
i cant rmb much about this... however i do remember that i used the accurate drawing method to solve this. just rmb AB is resultant.Originally posted by Y_Shun:Continued from the previous thread...
An aircraft flies due east from A to B where AB = 200km. The wind is blowing from the direction 030° at 60km/h. The speed of the aircraft in still air is 300km/h and the pilot sets the course on the bearing X°. Find
a) the value of X.
b) the time taken, in minutes for the journey from A to B.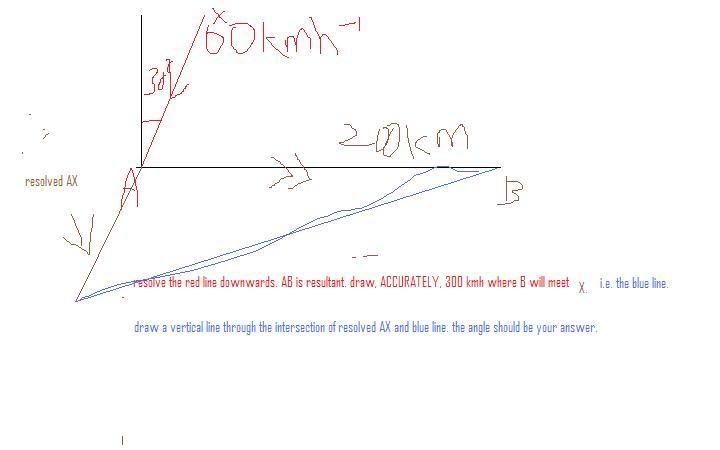
-
v. hard

can i forgo this topic and do good in other topics? still can get a1

-
not if u want to do well in physics too.Originally posted by Y_Shun:v. hard
can i forgo this topic and do good in other topics? still can get a1

and not if u going to poly/jc/uni
It's the basic foundation in vectors -
yes. most schools forgo it(im assuming you're doing o levels this yr). i didnt study for RV and got a1.Originally posted by Y_Shun:v. hard
can i forgo this topic and do good in other topics? still can get a1

-
RV ranges from 6 to 13 marks.
I'm planning to do the basic questions only. Apply sin rule, cos rule etc. -
And in aviation, we tend to resolve vectors in 3 diemensions.
-
So u are a aeronautical engineer? wow...Originally posted by Herzog_Zwei:And in aviation, we tend to resolve vectors in 3 diemensions.
anyway TS was just asking an O level question, and the aircraft was just one example of Cambridge testing the concept of Bearings. Not so chim yet
-
Not exactly, just did something on aviontronics.... Why certain safety devices wouldn't beep even if aircraft is way below required safety level.Originally posted by eagle:So u are a aeronautical engineer? wow...
anyway TS was just asking an O level question, and the aircraft was just one example of Cambridge testing the concept of Bearings. Not so chim yet
-
can someone explain part B to me more clearer??? as in the way a sec4 student do lol...its really too hard this topic.
no wonder they removing it for A level =[ -
try to find the angle opposite the black line, then use sine rule or cosine rule to get the length of the black line which is representative of the velocity.

-
I found it and used 200 divide by it, but i never get the ans.Originally posted by nightzip:try to find the angle opposite the black line, then use sine rule or cosine rule to get the length of the black line which is representative of the velocity.
-
i just double checked, answer is correct 75min.
please use 60/sin 10 = x/sin 50,
rearrange, you get x = (60sin50)/sin10
= 266.something....
so, 200/266... = 0.75.
Angle for 10deg is from (90-x) = (90-80)=10
Angle for 50deg is from (x-30)=(80-30)= 50.

-
i dun understand how u get 50 leh... and how come use 50>?
my diagram same as unclebutcher one...