Plane Geo (II)
-
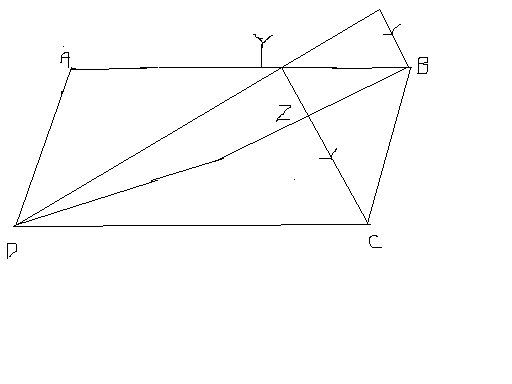
In the diagram, ABCD is Y is te midpoint of AB. XYD is a straight line and Z is the point of intersection of DB and YC. Given that XB is paralle to YC, prove that
(a) triangle YDC is similar to triangle XYB
(b) DY = 2 YX
(c) DZ = 2 ZB
I will provide you with my full solution before the sketch itself(which I drew using the paint programme). So pardon me for the bad drawing!
For (a)
since XB // YC
angleDYC = angle YXB (corres.)
angle YCD = angle XBY(corres. angle)
Hence the triangles are similar (angle-angle-angle similarity)
For (b)
since YC //XB, and Y is midpoint of AB
YC : XB = 2:1 (midpoint theorem)
since triangle YDC and triangle XYB are similar,
YC:XB = DY:YX = 2:1
.: DY = 2 YX (proven)
For (c)
triangle YDC is similar to triangle XYB(from(b))
triangle XDB is similar to triangle YDZ
from (b), we know that
YD:XY = 2:1
YD:XD = YD : (YD+XY) = 2:3
XD:YD = DB:DZ = (DZ+ZB):DZ
= 3:2
.:ZB = 1
Hence DZ = 2 ZB
Hang on, there's another one which I want to check whether the method is valid. (: thanks for your patience.
-
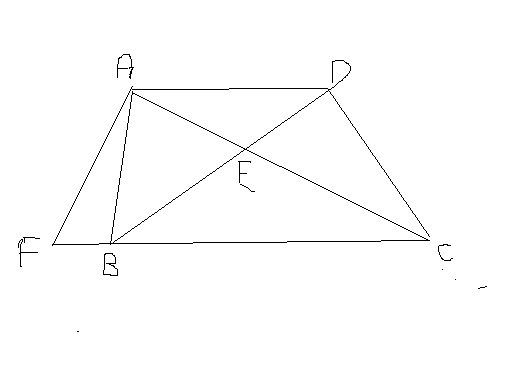
In the trapezium ABCD, AD is parallel to BC, BC = 3AD and the diagonals AC and BD meet at E. The line through A is drawn parallel to DB to meet the extended line of CB at F. Prove that
(a) FB = AD
(b) EC = 3AE
Again, the solutions first.
(a) Triangle AED is similar to triangle CEB
AD : CB = 1:3
CB:BF = CE:EA = CE: DA(intercept theorem)
since BF = DA based on above equation, FB = AD
(b) Since triangle AED is similar to triangle CEB
CB:BF = CE:EA=CB:AD = 3:1
hence EC = 3 AE(proven)
that's all. thank you once again.