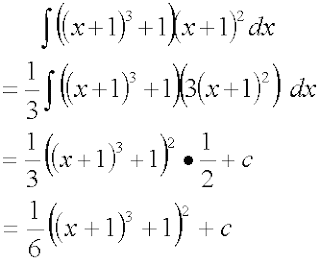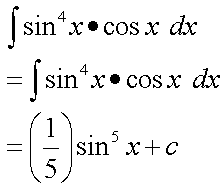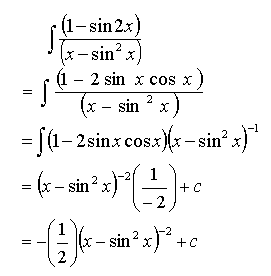Integration Questions
-
These questions are actually "O" level additional mathematics integration questions but these questions are more tricky.
Questions
(1) Integrate [(x+1)^3+1]^3(x+1)^2
(2) Integrate (x^5 + 1)/(x+1)
(3) Integrate 2 sin^2x
(4) Integrate sin^4x cosx
(5) Integrate (1-sin2x)/(x-sin^2x)Thank you for your kind attention.
Regards,
ahm97sic
-
-
I'll just do the first 3 questions for this.



-
Originally posted by ^tamago^:
I'll just do the first 3 questions for this.



Hi Tamago,
You don't have to expand out to integrate the first question. There is a shortcut to integrate it, the answer is very simplified. Hint: Use the reversal method.
Thank you for your kind attention.
Regards,
ahm97sic
-
these questions seems more like A level integration last time... Doesn't seem like the very standard O level
-
-
Hi Eagle,
Basically, these questions use the reversal method but these questions are just more tricky.
"O" Level add maths also test on the use of reversal method.
Actual past "O" level add maths questions on the use of reversal method
(1) Differentiate 1/[(9 - 4x^2] and then integrate x/[(9 - 4x^2]^2
(2) Differentiate xsinx and then integrate xcosx
(3) Differentiate x^3lnx and then integrate x^2lnx
(4) .......
Indeed, with the addition of partial fraction and further trigonometry, more varieties of questions can be set on integration eg integrate (17x^2 +23x + 12)/[(3x+4)(x^2+4) in the new 2008 syllabus of Additional Mathematics.
Thank you for your kind attention.
Regards,
ahm97sic
PS : Hi Eagle, you have copied the first question incorrectly ie you have ommitted the power 3. However, based on the question you copied, your answer is correct. You have forgotten to type the dx in your answer for question 5 and you have made a mistake in your answer to question 5 ie when you differentiate your answer, you cannot get back (1-sin2x)/(x-sin^2x), not due to the constant c, it is the power of -2. When we differentiate it, the power of -2 becomes -3, not -1.
Hint : Use logarithm ln
-
Originally posted by Ahm97sic:
Hi Tamago,
You don't have to expand out to integrate the first question. There is a shortcut to integrate it, the answer is very simplified. Hint: Use the reversal method.
Thank you for your kind attention.
Regards,
ahm97sic
Q1.

Q5.
What's the purpose of this thread? -
oops
sry... careless... I did everything mentally on MS word... Changed the answers on my blog liao
damn sleepy doing up ExamWorld
-
all use chain rule reversal method...
-
Originally posted by ^tamago^:
Q1.

Q5.
What's the purpose of this thread?Hi Tamago and Eagle,
The purpose of these integration questions is let students who are doing Add Maths to know (and try to solve) of the more tricky questions especially with the addition of partial fraction, further trigonometry in the new syllabus that can led to more varieties of questions to be set in the "O" level exam.
Eagle and Tamago, both of you have kindly worked out the solutions to these questions for the benefits of the "O" level Add Maths students.
Indeed, the homework forum should not just help to do the homework for the students, the forum should also encourage more students to visit the forum by providing exam questions (with provided solutions), exam tips, types of questions and the different ways how a topic are being set in the PSLE, "N" Level, "O" level and "A" level. Currently, the forum is a bit messy, it should be organised into different sub-headings eg Lower Primary, Upper Primary, PSLE, lower secondary, upper secondary, "N" Level, "O" Level, "A" Level and others.
Students should be encouraged to post interesting (ie tough) questions that they encountered in their schools so that students from other schools should also be able to try to solve and benefit from these interesting questions.
Hope that my suggestions will be of help.
Thank you for your kind attention.
ahm97sic
PS : Hi Tamago, you have used the "A" level substitution method to do the integration but the "O" level add maths students have not learnt this method, they are only taught the reversal method to do the integration.
-
Never heard of reversal method. Maybe you can share with us? :D
-
Indeed, the homework forum should not just help to do the homework for the students, the forum should also encourage more students to visit the forum by providing exam questions (with provided solutions), exam tips, types of questions and the different ways how a topic are being set in the PSLE, "N" Level, "O" level and "A" level. Currently, the forum is a bit messy, it should be organised into different sub-headings eg Lower Primary, Upper Primary, PSLE, lower secondary, upper secondary, "N" Level, "O" Level, "A" Level and others.
We are not in control on the sub headings of the forum.
And not possible to have all questions of the same level in a single thread. This is because students might ask more about the questions, or we might be handling a few questions at a time. It will greatly confuse the students if we do that.
That's why I set up ExamWorld ;)
-
Originally posted by ^tamago^:
Never heard of reversal method. Maybe you can share with us?

Hi Tamago,
Let's use an actual past "O" level question as an illustration of the reversal method.
Example
Differentiate 1/[(9 - 4x^2] and then integrate x/[(9 - 4x^2]^2
Let y = 1 / [(9 - 4x^2]
dy/dx = - 8x / [(9 - 4x^2]^2
To integrate x/[(9 - 4x^2]^2, we will try to make x/[(9 - 4x^2]^2 to be same as the dy/dx answer ie - 8x / [(9 - 4x^2]^2,
Integrate x / [(9 - 4x^2]^2
= -1/8 integrate - 8x / [(9 - 4x^2]^2
Without doing any integration, by reversal ie we know integrate dy/dx = y, so
= - 1/8 {1 / [(9 - 4x^2]}
Thank you for your kind attention.
Regards,
ahm97sic
PS : Hi Tamago, "O" Level add maths students have not learnt the "A" level substitution method to do the integration, they are only taught to use the reversal method to do the integration.
Using the reversal method to integrate, there is no need to have the constant c in the answers as it is an exact reversal of y.
-
ahm97sic
would like to invite you to join in at ExamWorld. :D
I can put an advertisement for your tuition services right under the subjects section, above the google search function. Currently looking for tuition teachers to help in posting and categorising for free advertisements.
-
Originally posted by eagle:
oops
sry... careless... I did everything mentally on MS word... Changed the answers on my blog liao
damn sleepy doing up ExamWorld
Hi Eagle,
Using the reversal method to integrate, there is no need to have the constant c in the answers as it is an exact reversal of y.
Thank you for your kind attention.
Regards,
ahm97sic
-
Originally posted by Ahm97sic:
Hi Eagle,
Using the reversal method to integrate, there is no need to have the constant c in the answers as it is an exact reversal of y.
Thank you for your kind attention.
Regards,
ahm97sic
I believe the constant c is still required.
It is only not required if it is a definite integral.
Correct me if I'm wrong. Thanks.
-
Hi Eagle,
Let's use a simplified example
y = 2x^3 + 5
dy/dx = 6x^2
If y is not given at first and we are asked to integrate 6x^2,
Integrate 6x^2
= (6x^3)/3
= 2x^3
There is no way to get the 5 in the original y, so there is a need to add the constant c to represent a possible constant in the original y, so
= 2x^3 + c
But when the question asks
Differentiate y = 2x^3 + 5 and integrate 7x^2
y = 2x^3 + 5
dy/dx = 6x^2
To integrate 7x^2, we try to make 7x^2 to be the same as the dy/dx answer ie 6x^2.
Integrate 7x^2
= 7/6 integrate {6x^2}
Without doing any integration, by reversal integrate dy/dx = y,
= 7/6 {2x^3 + 5}
Thus, the 5 in the original y is accounted for and so there is no need to have the constant c to represent a possible constant in the original y (as in the case of the indefinte integral).
Thank you for your kind attention.
Regards,
ahm97sic
-
Originally posted by Ahm97sic:
Hi Eagle,
Let's use a simplified example
y = 2x^3 + 5
dy/dx = 6x^2
If y is not given at first and we are asked to integrate 6x^2,
Integrate 6x^2
= (6x^3)/3
= 2x^3
There is no way to get the 5 in the original y, so there is a need to add the constant c to represent a possible value in the original y.
But when the question asks
Differentiate y = 2x^3 + 5 and integrate 7x^2
y = 2x^3 + 5
dy/dx = 6x^2
To integrate 7x^2, we try to make 7x^2 to be the same as the dy/dx answer ie 6x^2.
Integrate 7x^2
= 7/6 integrate {6x^2}
Without doing any integration, by reversal integrate dy/dx = y,
= 7/6 {2x^3 + 5}
Thus, the 5 in the original y is accounted for and so there is no need to have the constant c to represent a possible value in the original y (as in the case of the indefinte integral).
Thank you for your kind attention.
Regards,
ahm97sic
The reason for adding + c is because it is a general case.
If you differentiate 7/6 {2x^3 + 5}, you get 7x^2
but if you differentiate 7/6 {2x^3 + 5} + c, you still get 7x^2
This is because c can be 7/6 * 5 or any other value.
That's the reason for adding + c for indefinite integrals.
Not sure if you are referring to the questions in the first post... or other questions...Even then, for questions that ask for differentiate, then integrate... a +c is still required. This is because the first part of the question serves to guide the student to be able to integrate in the 2nd part of the question. I don't really think they are linked.
-
Originally posted by eagle:
The reason for adding + c is because it is a general case.
If you differentiate 7/6 {2x^3 + 5}, you get 7x^2
but if you differentiate 7/6 {2x^3 + 5} + c, you still get 7x^2
This is because c can be 7/6 * 5 or any other value.
That's the reason for adding + c for indefinite integrals.
Hi Eagle
Reversal Method Indefinte Integration Method
y = 2x^3 + 5 Integrate 6x^2
dy/dx = 6x^2 = (6x^3)/2 + c
Integrate dy/dx =y = 2x^3 + c
Integrate 6x^2
= 2x^3 + 5
Please take another look at the two methods.
The reversal method is able to get back the constant 5 because the original y is given while the indefinte integration method is unable to get the constant 5 because the original y is not given and hence a constant c is used to represent the possible constant as in the case of indefinite integral.
Reversal Method Indefinte Integration Method
y = 2x^3 + 5 Integrate 7x^2
dy/dx = 6x^2 = (7x^2)/3 + c
Integrate dy/dx = y = 7/3 x^2 + c
= Integrate 7x^2
= 7/6 integrate {6x^2}
= 7/6 {2x^3 + 5}
= 7/3 x^2 + 35/6
The reversal method is able to give the exact constant 35/6 because the original y is given while the indefinte integration method is unable to get the constant 35/6 because the original y is not given and hence a constant c is used to represent the possible constant.
Thank you for your kind attention.
Regards,
ahm97sic
-
I think I get what you mean
But I still don't think this should be the full answer. The logic still doesn't sound right. To me, if y = 2x^3 + 5, and dy/dx = 6x^2,
integrate dy/dx = integrate 6x^2 should give me 2x^3 + c, not 2x^3 + 5. It's to me like... a square is a rectangle, but a rectangle is not a square. At the very least, we should find back the value of c when we are given an equation to get a resultant c, and not because we are given y, find dy/dx, then integrate to get back c automatically as 5. To me, the logic just does not flow.
 Maybe it would make sense if a scenario in physics or other stuff is given, but if we are just given equations in maths as the symbols, then I don't think so....
Maybe it would make sense if a scenario in physics or other stuff is given, but if we are just given equations in maths as the symbols, then I don't think so....But I guess... Since this is what they teach in A maths... we have to coach the students this way...

y = 2x^3 + 5
dy/dx = 6x^2
Integrate dy/dx = y
= Integrate 7x^2
= 7/6 integrate {6x^2}
= 7/6 {2x^3 + 5}
= 7/3 x^3 + 35/6
Not very sure about the part in red...
if integrate dy/dx = 7, and dy/dx = 6x^2,
then y should be 2x^3 + 5, not integrate 7x^2
How come for the same y, it is used for 2 different equations?
Thanks for being so patient to tell me about the new syllabus :D
-
Hi Eagle
The difference between the two methods is something like there are two ball bearings, one large and one small.
There are two pipes, one large and one small.
Case 1 (Indefinite Integration Method)
Only the large ball bearing passes through a large pipe (the small ball bearing is assumed to be stucked and it does not pass through the small pipe) and the large ball bearing is being melted when it passes through the pipe. Indefinite integration is something like with the melted iron, we will remould it into the large ball bearing. We know that there is the small ball bearing but it is assumed to be stucked and so there is no melted iron of the small bearing, so we will not be able to remould the small ball bearing but we know that we have a small ball bearing at first, so we have to add the constant c in the indefinite integration method.
Case 2 (Reversal Method)
Both ball bearings pass through the pipes and they are being melted when they pass through the pipes. Reversal Method is something like with the melted iron, we will be able to remould the large and small ball bearings ie an exact reversal, so there is no need to add the constant c in the reversal method.
Example 1
A typical question that requires A typical question that requires the use of
the use of reversal method is indefinite integration method
(1) Given that y = 2x^3 + 5 (1) y function is not given ie y = 2x^3 + 5 is
(2) Differentiate y = 2x^3 + 5 not given
(3) Next, integrate 6x^2 (2) Integrate 6x^2
Reversal Method Indefinte Integration Method
(1) Given y = 2x^3 + 5 (1) y = 2x^3 + 5 is not given
dy/dx = 6x^2
(2) Next, integrate 6x^2 (2) Integrate 6x^2
(use integrate dy/dx = y) = (6x^3)/2 + c
= 2x^3 + 5 = 2x^3 + c
Important Note :
Mathematically, when we integrate 6x^2 = 2x^3 but in the case of the reversal method, we are given the information that the original y has the constant 5, so the answer is 2x^3 + 5. However, in the case of indefinite integration method, there is no given information that the original y has the constant 5 since the original y is not given, so the constant c is used to represent the 5 in the original y in the answer ie 2x^3 + c.
Please take another look at the two methods.
The reversal method is able to get back the constant 5 because the original y is given while the indefinte integration method is unable to get the constant 5 because the original y is not given and hence a constant c is used to represent the possible constant as in the case of indefinite integral.
Example 2
Reversal Method Indefinte Integration Method
(1) Given y = 2x^3 + 5 (1) y = 2x^3 + 5 is not given
dy/dx = 6x^2
(2) Next, integrate 7x^2 (2) Integrate 7x^2
= 7/6 integrate {6x^2} = (7x^2)/3 + c
(use integrate dy/dx = y) = 7/3 x^2 + c
= 7/6 {2x^3 + 5}
= 7/3 x^2 + 35/6
The reversal method is able to give the exact constant 35/6 because the original y is given while the indefinte integration method is unable to get the constant 35/6 because the original y is not given and hence a constant c is used to represent the possible constant.
Thank you for your kind attention.
Regards,
ahm97sic
-
I understand what you mean, but I still think that the logic is not totally correct. At least for levels higher than O levels, this will be an inadequate answer... This is because the question do not state any limitations in this case... Just like Newton's 2nd law... O levels learn only half of the actual meaning.... But at A levels, it is learned more in depth... I guess this is what's happening now.
Anyway,
The first part I understand is
y = 2x^3 + 5
dy/dx = 6x^2
so integrate dy/dx = y = 2x^3 + 5This part I agree...
but 2nd part I don't fully understand is
y = 2x^3 + 5
dy/dx = 6x^2
Integrate 7x^2 = 7/6 integrate 6x^2
= 7/3 x^2 + 35/6So we are now actually finding 7y/6 instead of y. Is it correct?
Thanks...!
P.S. Is there any other websites in which I can read up more on the reversal method? When I try to google it, it comes up sgforums...

-
Originally posted by eagle:
I understand what you mean, but I still think that the logic is not totally correct. At least for levels higher than O levels, this will be an inadequate answer... This is because the question do not state any limitations in this case... Just like Newton's 2nd law... O levels learn only half of the actual meaning.... But at A levels, it is learned more in depth... I guess this is what's happening now.
Anyway,
The first part I understand is
y = 2x^3 + 5
dy/dx = 6x^2
so integrate dy/dx = y = 2x^3 + 5This part I agree...
but 2nd part I don't fully understand is
y = 2x^3 + 5
dy/dx = 6x^2
Integrate 7x^2 = 7/6 integrate 6x^2
= 7/3 x^2 + 35/6So we are now actually finding 7y/6 instead of y. Is it correct?
Thanks...!
P.S. Is there any other websites in which I can read up more on the reversal method? When I try to google it, it comes up sgforums...

Hi Eagle,
In the second example, the question requires us to differentiate y = 2x^3 + 5 and next the question requires us to make use of the answer to integrate 7x^2.
Integrate 7x^2
= 7/6 Integrate 6x^2
= 7/6 Integrate dy/dx (since dy/dx = 6x^2)
= 7/6 y (since integrate dy/dx = y)
= 7/6 {2x^3 + 5} (since y = 2x^3 + 5)
= 7/3 x^2 + 35/6
Sorry, my explanation has not been clear and get you confused, when I type " use integrate dy/dx = y", I mean the portion in red. Please accept my apologies.
Thank you for your kind attention.
Regards,
ahm97sic