Tough plane geo question

• bonkysleuth

  13 May 09, 13:19

  In the triangle ABC, BF and CE are perpendicular to AC and AB respectively.  D and G are the midpoints of EF and BC respectively. Prove that GD is perpendicular to EF.

   

  

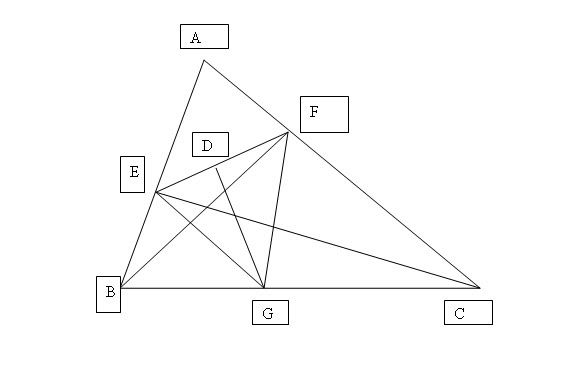
  Been doing plane geo questions since morning. argh, driving me crazy. Can someone tell me how to score for such questions? TYS answers are as good as not giving at all. The more questions on plane geo I do, the more insecure and less confident I become... having a maths exam tomorrow and my teacher said plane geo question is worth 9 marks.

   

  thanks everyone

   

  Edited by mod for Typos.

• skythewood

  13 May 09, 17:51

  I try to find the triangle ABD. I failed.

• yiha093

  13 May 09, 20:01

  use triangle properties ? 

• eagle

  13 May 09, 21:05

  ok this question took me about 5+ mins to solve, quite tough... :(

  dot a perpendicular line from G to BE and label it as H
  dot a perpendicular line from G to FC and label it as I
  
  Note that by similar triangles,
  
  consider triangles HBG and EBC
  because BG = ½BC,
  EH = ½BE
  HG = ½EC

  
  consider triangles GIC and BFC
  because BG = ½BC,
  FI = ½FC
  GI = ½BF

  Thus,

  EG² = EH² + HG²
  = ¼BE² + ¼EC²
  = ¼BC²

  GF² = GI² + FI²
  = ¼BF² + ¼CF²
  = ¼BC²
  = EG²

  Thus, GF = EG

  Since GF = EG, and ED = DF, then GEF is an isosceles triangle where GD is perpendicular to EF

• wee_ws

  13 May 09, 21:51

  Hi eagle,

    Clever!

    After drawing the extra lines (we call them auxiliary lines), we can use the intercept theorem directly. Then it is followed by the application of Pythagoras' theorem.

    Thanks for sharing!

  Cheers,
  Wen Shih

• eagle

  14 May 09, 00:03

  Thanks Wen Shih

   

  I have drawn out the answer and placed it on examworld

   

  

   

  Enjoy :D