Plane Geometry
-
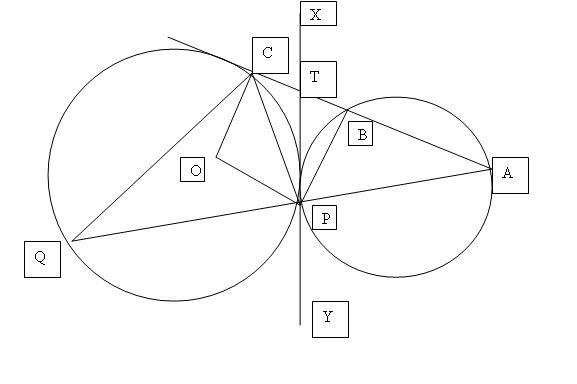
In the diagram, XTPY is a tangent to 2 circles at P and ABTC is a tangent to the circle of centre O at C.
The line AP is a chord of one circle and produced to meet the other circle at Q.
Ok, part 1 of the question asks
explain why a circle passes through O,C, T and P
Thanks!
-
Originally posted by anpanman:

In the diagram, XTPY is a tangent to 2 circles at P and ABTC is a tangent to the circle of centre O at C.
The line AP is a chord of one circle and produced to meet the other circle at Q.
Ok, part 1 of the question asks
explain why a circle passes through O,C, T and P
Thanks!
I hope you will not be offended by this, but I strongly suggest that you work on your model drawing skills. After staring at your model for quite a while, I realised that some points are drawn very off-scale.
Back to your question,
OCT and OPT = 90 degree each, as XTPY and ABTC are both tangents to the circle with center O at C and P respectively.
OC = OP, as both of them are radius of the circle with center O.
= > OCTP is a square. And since it is a square, it is possible for a circle to pass through O, C, T and P.
-
i think he meant this

and OCTP is not a square coz i got the question
-
Originally posted by Forbiddensinner:
I hope you will not be offended by this, but I strongly suggest that you work on your model drawing skills. After staring at your model for quite a while, I realised that some points are drawn very off-scale.
Back to your question,
OCT and OPT = 90 degree each, as XTPY and ABTC are both tangents to the circle with center O at C and P respectively.
OC = OP, as both of them are radius of the circle with center O.
= > OCTP is a square. And since it is a square, it is possible for a circle to pass through O, C, T and P.
Shi fu why u so ge zhou : X
let TO be diameter, and since oct and opt are 90degrees a circle pass through octp.
-
Originally posted by Forbiddensinner:
I hope you will not be offended by this, but I strongly suggest that you work on your model drawing skills. After staring at your model for quite a while, I realised that some points are drawn very off-scale.
Back to your question,
OCT and OPT = 90 degree each, as XTPY and ABTC are both tangents to the circle with center O at C and P respectively.
OC = OP, as both of them are radius of the circle with center O.
= > OCTP is a square. And since it is a square, it is possible for a circle to pass through O, C, T and P.
Hi. But how do you just prove that OCTP is a square? You haven't yet shown that TC = TP=OP=OC you merely proved that OC=OP(radius) and that they are 90 deg. It could be a rectangle...thanks!
The side of TC and TP are neglected
-
Originally posted by ??aaa??Wwqa:
i think he meant this

and OCTP is not a square coz i got the question
Yea, the diagram drawn is exact. OCTP is not a square. Thanks for going through the hassle of drawing again!PS: you forgot to link point Q to C
-
Originally posted by anpanman:
Hi. But how do you just prove that OCTP is a square? You haven't yet shown that TC = TP=OP=OC you merely proved that OC=OP(radius) and that they are 90 deg. It could be a rectangle...thanks!
The side of TC and TP are neglected
Sorry, but my answer was incorrect. Indeed all the points listed were not enough to prove that OCTP is a square.
The one given by my tutee should more or less give you an idea how to prove it though.
-
Originally posted by Forbiddensinner:
Sorry, but my answer was incorrect. Indeed all the points listed were not enough to prove that OCTP is a square.
The one given by my tutee should more or less give you an idea how to prove it though.
Yes, it does. (: I looked at it for quite some time and realised it was 2 semicircles. Thanks! -
Originally posted by Forbiddensinner:
Sorry, but my answer was incorrect. Indeed all the points listed were not enough to prove that OCTP is a square.
The one given by my tutee should more or less give you an idea how to prove it though.
Yes, it does. (: I looked at it for quite some time and realised it was 2 semicircles. Thanks! -
Let angle COP=2x
Hence angle CQP=x ( angle at centre = 2 angle at circumference)
angle PCB = angle CQP =x (alt. seg. them.)
also, angle CPT= angle CQP=x (alt. seg. them.)
Hence, angle CTP= 180-2x (sum of angles in triangle)
As, angle COP + angle CTP=180,
quad.CTPO is a cyclic quad, at which a circle will pass through all of the points.