A level Maths - Vectors

• Audi

  11 Aug 10, 20:49

  Relative to an origin O, the position vectors of points A and B are a and b respectively. Givent that angle AOB is 90deg, show that the position vector of the foot of the perpendicular from O to AB is

  a  +  (|a|^2 / (|a|^2 + |b|^2))  (b-a)

  Need help for this question. Thanks!

• Mad Hat

  12 Aug 10, 00:05

  

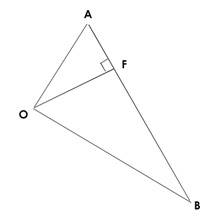
  Let F be the foot in question. Notice that OF = OA + k(AB), where k is an unknown fraction.

  In other words, OF = a + k(b−a).

  To answer the question, we simply need to find k, so let's do it.

  Since OF is perpendicular to AB, it follows that OF · AB = 0.
  So ( a + k(b−a) ) · (b−a) = 0.

  Simplify and re-arrange to solve for k. (Your "vector algebra" is being tested.)

• SBS261P

  12 Aug 10, 01:19

  ^beautifully done.

  alternatively A level students are also taught the ratio theorem. you can try applying ratio theorem here.

• wee_ws

  12 Aug 10, 08:36

  Hi,
  
    This type of question may be back in vogue, now that Cambridge may have exhausted its list of numerically-based questions that can be asked.
  
    Here is one question that involves vector product algebra as well as trigonometry:
  
    With respect to the origin O, point P has position vector given by p = −2i + j + k and the variable point Q has position vector given by q = (cos t)i + 2j , where 0 <= t <= pi. Show that
  |p x q| = sqrt [ 2(cos t  + 2)^2 + 12 ]. Hence find the smallest exact area of triangle OPQ.
  
    The approach to deal with questions involving variables is to use the USUAL manner of solving numerically-based problems.
  
    Thanks.
  
  Cheers,
  Wen Shih

• eagle

  12 Aug 10, 09:12

  Originally posted by Mad Hat:

  

  Let F be the foot in question. Notice that OF = OA + k(AB), where k is an unknown fraction.

  In other words, OF = a + k(b−a).

  To answer the question, we simply need to find k, so let's do it.

  Since OF is perpendicular to AB, it follows that OF · AB = 0.
  So ( a + k(b−a) ) · (b−a) = 0.

  Simplify and re-arrange to solve for k. (Your "vector algebra" is being tested.)

  Alternatively, we can make use of vector projection to solve.

  OF = OA + AF = a + |a| cos θ * (b - a) / |b - a|, where θ = angle between OA and BA

  = a + |a| [ {a.(a - b)} / {|a| |a - b| }] * (b - a) / |b - a|

  = a +  {a.a - a.b} / (|a|^2 + |b|^2) * (b - a)

  = a +  |a|^2 / (|a|^2 + |b|^2) * (b - a) since a.a = |a|^2 and a.b = 0

   

  Thanks :)

• wee_ws

  12 Aug 10, 12:33

  Hi eagle,

    Great work! Thanks for sharing :)

  Cheers,
  Wen Shih